Details
I was expecting to have some difficulty creating draggable buttons in AS3 in this Widget, but found that it was easier than creating them in AS2. The most noteworthy part of this Widget is the way the compass needle follows the tangent to the curves of the magnetic fields. To do this I decided to use trigonometry, as each magnetic field outside the magnet core is the shape of an elipse. If they were circles, my calculations would have been a bit easier. I could have easily found the center point of each circle to use as the starting point for the trigonometric calculations. But, because they are elipses, I needed to find the two foci (similar to center points) of each elipse. The positions of the foci of an elipse are relative to the ratio between the longest and shortest diameters. If you draw a line from each foci that intersect the circumference of the elipse (I'll call these lines e_radii), the sum of the length of those two lines is equal to the the longest diameter. So by using the equation:
longestDiameter.length = e_radii_1.length + e_radii_2.length
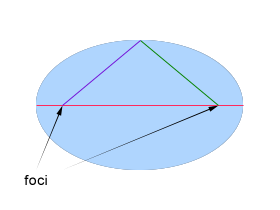
I was able to find the positions of the two foci. I did this by dynamically drawing a horizontal line that's length is half the width of the elipse, starting at the top center of each elipse. I then rotated the line down incrementally keeping it's rotation point at the top center of the elipse. After each incremental rotation I checked to see if that line's y coordinate plus it's height equalled the y coordinate of the elipse's horizontal mid point. In other words, I created an e_raddi that is half the diameter of the elipse, and rotated it until it met the horizontal diameter. That point where the e_raddi intersects the diameter is where the elipse's foci should be. I just needed to add the other foci the same distance in at the other side of the elipse.
After finding the foci points of each elipse, I could then determine the tangent of any point on the elipse's edge. I used a collision test between the compass center and the magnetic fields to determine which elipse to use to get the calculations from.
When the compass was over an elipse, I dynamically drew lines from each of that elpse's foci points to the center of the compass. Then I had a triangle to work with. I then dynamically drew a vertical line from the compass center to the elipse's horizontal diameter. I then had two sides that met at 90 degrees. SO I could use Pythagoras' Theorum to determine the remaining angle sizes and side lengths of the triangles I had created (since I could easily measure the length of two sides of each triangle ie the distance between the foci and the vertical distance from the compass to the horizontal diameter). With all this data I had calculated, it was then just a matter of finding the angle that sits half way between the the angles of the two dynamiaclly drawn e_radii, where they meet the copass center. The tangent is 90 degrees to that angle.
Drag the compass to see the calculations for determining the needle direction
So then, I just had to rotate the compass needle to the tangent angle. I smoothed out the compass needle's rotation animation by giving in a dynamic eased tween. I also used many more elipses (magnetic fields) than you can see (they are invisible, but still collision detectable) so that the compass had more reference points (foci) to perform calculations from.
In the end I think it worked very well. So well, that no one would really even think there is anything special going on in the background. It just looks like a compass shuld behave.
I worked closely with a physics subject matter expert while developing this series in order to make sure it was as scientifically correct as possible, while also working with educational specialists to make sure that it could be easily understood and delivered an effective learnign outcome.